Revista daESPM – Julho/Agosto de 2002
42
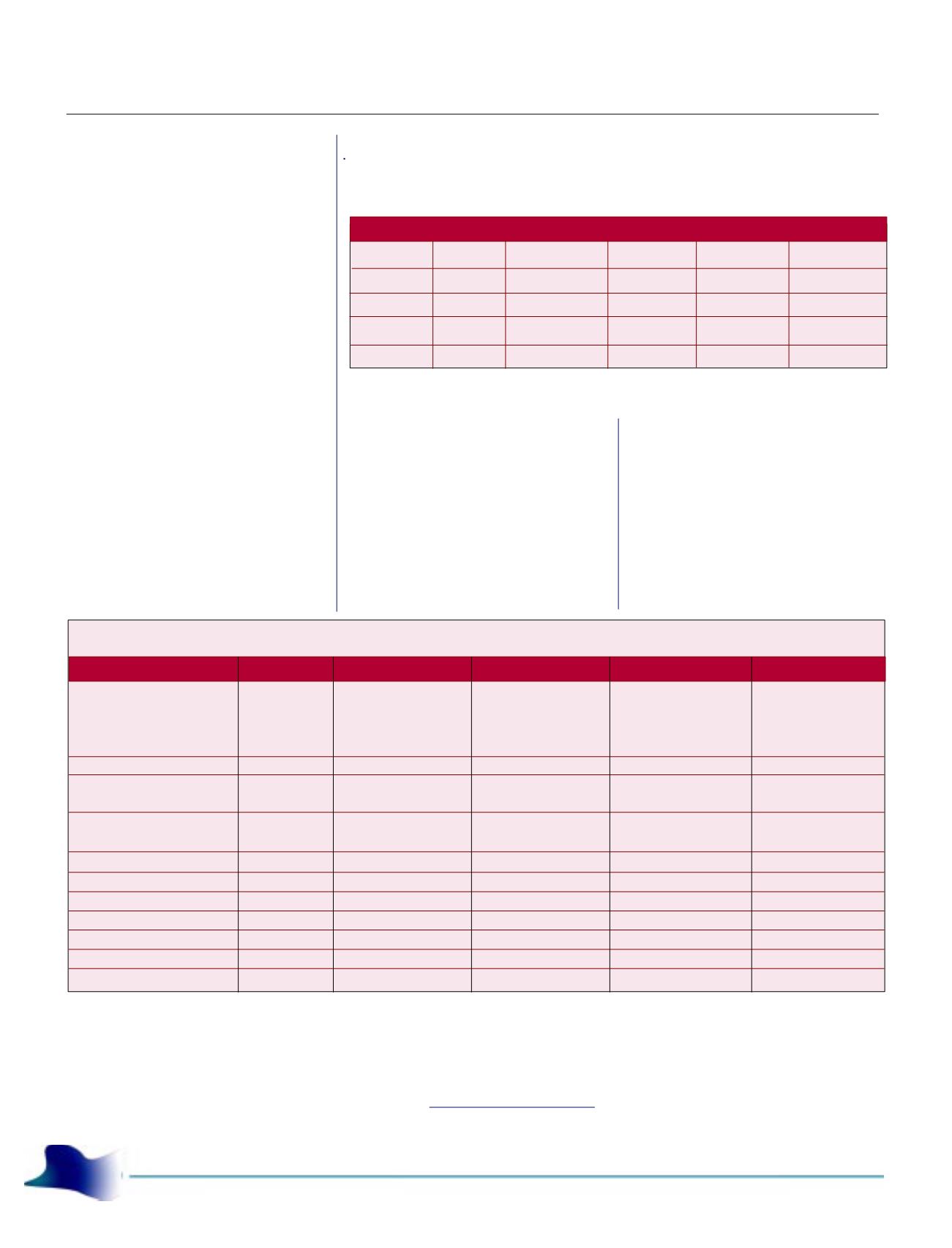
Tabela2:Valoresestimadosparaosconstructos
domodelodeFornell(1992).
Elaboradapelo autor.
Constructos
Expectativa
Valor
Satisfação
Voz do cliente
Fidelidade
Modelodo ano1998
73
76
63
78
61
Modelodo ano 1999
59
67
52
66
48
Modelodo ano 2000
59
62
59
42
62
Modelodo ano 2001
54
54
55
41
59
Modelo Geral
63
66
57
61
56
VI–Resultados
Segundo Li & Collier (2000), um
bom ajuste domodelo proposto requer
que todas as estatísticas de ajuste sejam
aceitáveis e os coeficientes estimados
sejam tambémaceitáveisestatisticamen-
te.Asestatísticasutilizadasnesteensaio
são as propostas pelo aplicativo
StatisticalAnalysisSystem
(SAS), epor
Latif (2000).
Essas estatísticas estão exibidas na
Tabela 1: Qui-quadrado, seus graus de
liberdade e sua probalilidade;
o root
mean square error aproximation
(RMSEA), quedevevariarpreferencial-
menteentre0,05e0,08;o
goodnessof fit
index
(GFI),quedeveserpróximode1,0;
o
normer fit index
(NFI), que também
deve estar próximode1,0. Por fim estão
listados os estimadores para os coefici-
entes domodelo, acompanhados de sua
estatística
t
e da quantidade de observa-
ções de cada ano.
A comparaçãodos resultados pode
ser mais bem estabelecida se analisa-
dos na forma de gráficos.A seguir se-
rão apresentados dois gráficos dos re-
sultados para os constructos domode-
lo. O primeiro reproduz a Figura 1,
agora com resultados numéricos. O
segundo é uma interpretação do com-
portamentodo consumidor, através de
uma figurageométrica, umgráfico em
três dimensões. Nesse gráfico, os
constructos foram reordenados para
possibilitar a construção de um figura
contínua, a variável tempo foi
desconsiderada, tomando o seu lugar
o comportamento do consumidor. O
objetivo dessa figura é proporcionar
uma interpretação para o comporta-
mento do consumidor, segundo omo-
delo adotado, de caráter atemporal.
Com os parâmetros acima estimados
foram calculados os valores para os
constructos
ξ
,
η
1 ,
η
2 ,
η
3 e
η
4domo-
delo exibido na Figura 1, pela fórmula
sugerida por Fornell et al. (1996) e tam-
Σ
w
i
.x
i
-
Σ
w
i
.Min (x
i
)
Constructo
j
=
Σ
w
i
.Max (x
i
) -
Σ
w
i
.Min (x
i
)
onde: w
i
= coeficiente de
regressão da variável x
i
.
x
i
= variável que
compõe o constructo j.
j = 1, ... , 5.
bém porMarchetti & Prado (2001). Es-
ses resultadosestãoexibidosnaTabela2.
Tabela1:ResultadosdomodeloracionalsobashipótesesH1aH6,usandooalgoritmoLISREL.
Elaboradapelo autor.
Estatística deAjuste
Chi-square and degrees
of freedom
Fit Finction < 1,0
p-value de ajuste
(RMSEA: 0.05 ~ 0.08)
Goodness of fit index
(GFI) ~ 1.0
γ
11
( t value )
γ
12
(t value)
β
21
(t value)
β
32
( t value )
β
42
(t value)
β
43
(t value)
n (casos válidos)
ModeloGeral
301,2
48
p<0,001
0,38
0,08
0,93
0,87 (37,7)
0,46 (41,3)
0,46 (47,6)
0,93 (34,9)
1,27 (90,8)
-0,27 (-20,5)
790
Modelo do ano 1998
113,1
48
p<0,001
0,45
0,06
0,93
0,65 (16,6)
0,42 (18,6)
0,42 (28,8)
0,57 (12,1)
0,92 (34,6)
0,47 (31,3)
254
Modelo do ano 1999
95,7
48
p<0,001
0,39
0,06
0,93
0,98 (23,4)
0,49 (27,2)
0,49 (27,7)
0,71 (19,1)
1,43 (69,6)
-0,61 (-41,5)
245
Modelo do ano 2000
129,4
48
p<0,001
0,99
0,11
0,83
0,81 (16,0)
0,22 (9,7)
0,53 (28,5)
1,11 (18,9)
0,21 (5,2)
0,97 (21,6)
131
Modelo do ano 2001
166,4
48
p<0,001
0,61
0,08
0,90
0,58 (13,5)
0,50 (17,5)
0,52 (31,1)
0,78 (12,8)
1,65 (63,6)
-0,53 (-26,3)
160


