Revista daESPM – Julho/Agosto de 2002
45
Apêndice1–
Variáveis
Latentes
McDonald (1997) propõe notação e
interpretação simples para as variáveis
latentes, que podem ser assim expres-
sas: Considere
v
um vetor aleatório de
variáveis observadas, de ordem (n x 1),
que são obtidas em uma amostragem.
Supõem-sequeE(
v
)=0.Umcasoespe-
cial deummodelo linear pode ser escri-
to assim:
v
=
B
.
v
+
e
,
sendo que (1)
cov(
v
) =
Σ
, e (2)
cov(
e
) =
Ψ
, onde cov éa
covariância da variável.
(3)
de tal modo que os elementos
β
jk
e
Ψ
jk
de
B
e
Ψ
sejam funções de um vetor de
ordem (tx1)deparâmetrossendoeo ter-
mo de erro.
De (1) tem-se que:
e= (
I –B
)
.v
, e (4)
v = (
I
–
B
)
–1
.
e
(5)
Definindo
A
= [
α
jk
]=
(I–B)
–1
, tem-
se que
(6)
Σ
= (
I –B
)
–1
e
Ψ
= (
I –B
)
T –1
ou,
reescrevendo segundo (6)
Σ
=
A
Ψ
A
T
e
(7)
Ψ
=
A
-1
Σ
A
T-1
(8)
Define-se
Φ
= cov (
v,e
) e de
(3)
e
(5)
tem-se:
Φ
=
A
.
Ψ
ou
Φ
=
Σ
(
I –B
)
T
(9)
Se a j-ésima linhade
B
énula, então
e
j
=
v
j
, com as variáveis reordenadas,
pode-se escrever (1) como um sistema
de equações:
A equação (12) é a representação
matricial domodelo de equações estru-
turais de variáveis latentes, onde:
η
=
vetor (m x 1) de variáveis
endóginas;
ξ
=
vetor (n x 1) de variáveis exóginas;
ε
=
vetor (m x 1) de erro nas equações;
B=
matriz (m xm) de coeficientes de
regressão das variáveis endógenas;
Γ
=
matriz (m x n) de coeficientes de
regressão das variáveis exógenas;
Φ
=
matriz (n x n) de covariância de
ξ
ξ
η
=
0
Γ
0
Β
∗
x
ξ
η
+
ξ
ε
,
ou
(11)
η
=B
Τ
.
η
+
Γ
.
ξ
+
ε
(12)
ε
3
ε
4
ε
5
e
Ψ
=
matriz(mxm)decovariânciade
ε.
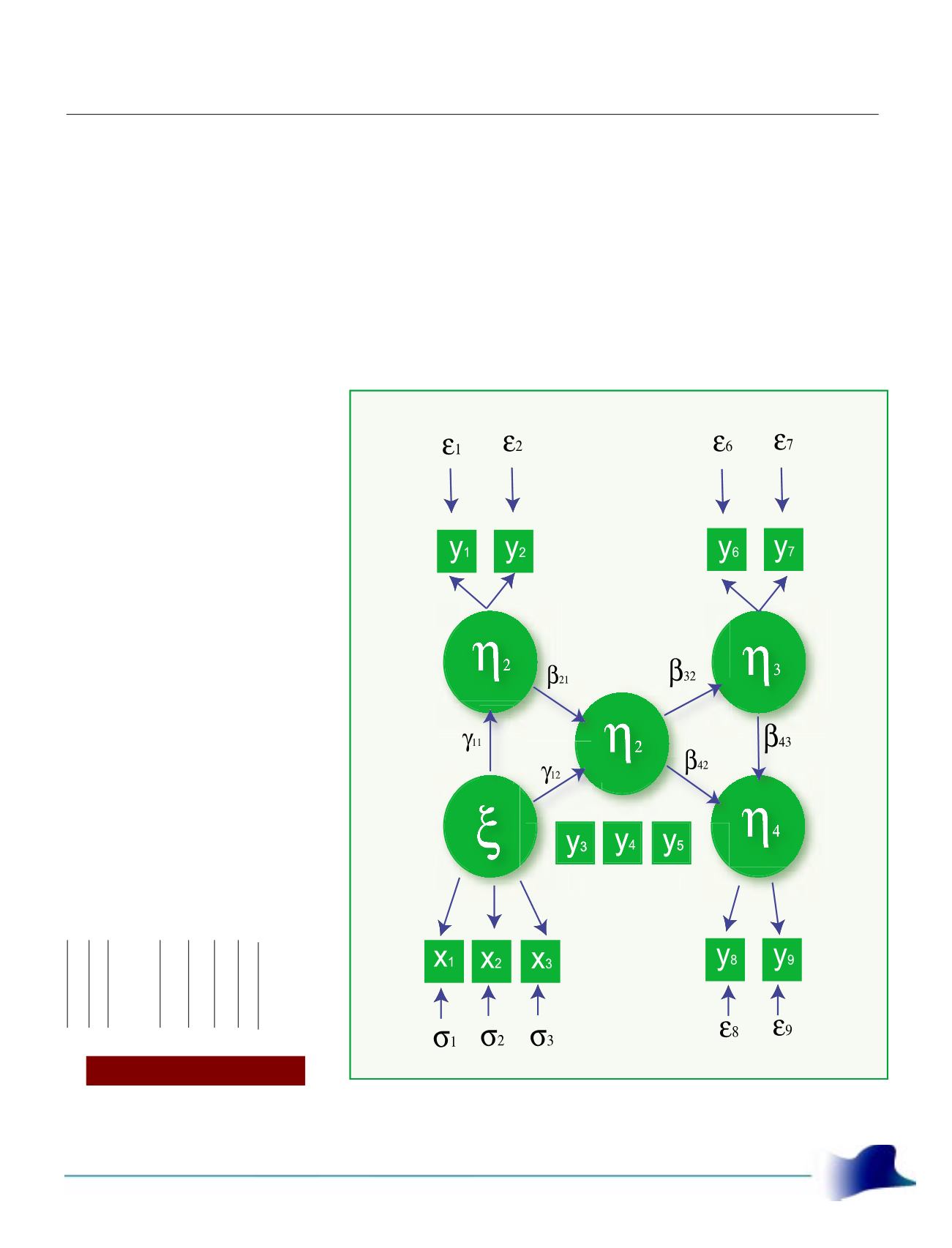
Bollen (1989) sugerequeummo-
delo causal seja, inicialmente, ex-
presso por meio de um diagrama de
raiz, onde as relações causa-e-efei-
to serão apontadas para, em segui-
da, especificar-se o modelo de aná-
lise estatística. Segundo essa pro-
posta, o Índice Nacional da Satisfa-
ção do Cliente – (INSC), proposto
por Fornell (1992), pode ser assim
escrito:
Figura 3: DiagramadeRaiz paraomodelodo ÍndicedeSatisfaçãodoCliente. Elabora-
dapeloautor.


